The modified Wald method for computing the confidence interval of a proportion

Statisticians have developed multiple methods for computing the confidence interval of a proportion.

The GraphPad QuickCalc for determining the confidence interval of a proportion uses two different methods, and reports the results for both. The first method was developed by Clopper and Pearson (1), and is offered by many statistics packages. The result is labeled an “exact” confidence interval (in contrast to the approximate intervals you can calculate conveniently by hand). Computer simulations demonstrate that the so-called exact confidence intervals are really approximations(2). The discrepancy varies depending on the values of S and N. The so-called “exact” confidence intervals are not, in fact, exactly correct. These intervals may be wider than they need to be and so generally give you more than 95% confidence.

The second method used by the GraphPad QuickCalc for determining the confidence interval of a proportion was developed by Agresti and Coull (3), which they term the modified Wald method. It is easy to compute by hand and is more accurate than the so-called “exact” method. The 95% CI is calculated using the following equation (note that the variable “p” as used here is completely distinct from p values) :

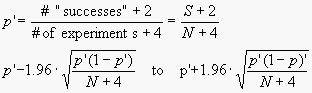
In some cases, the lower limit calculated using that equation is less than zero. If so, set the lower limit to 0.0. Similarly, if the calculated upper limit is greater than 1.0, set the upper limit to 1.0.

Where did the numbers 2 and 4 in the equation come from? Those values are actually z²/2 and z², where z is a critical value from the Gaussian distribution. Since 95% of all values of a normal distribution lie within 1.96 standard deviations of the mean, z = 1.96 (which we round to 2.0) for 95% confidence intervals.

Note that the confidence interval is centered on p', which is not the same as p, the proportion of experiments that were “successful”. If p is less than 0.5, p' is higher than p. If p is greater than 0.5, p' is less than p. This makes sense, as the confidence interval can never extend below zero or above one. So the center of the interval is between p and 0.5.

Agresti and Coull (3) showed that this method works very well, as it comes quite close to actually having 95% confidence of containing the true proportion, for any values of S and N. With some values of S and N, the degree of confidence can less than 95%, but it is never has less than 92% confidence.

GraphPad Prism

GraphPad Prism can also calculate the confidence interval of a proportion, but provides three different methods for their determination. One of these three methods is the "exact" method (Clopper and Pearson) described above and available in the GraphPad QuickCalc for determining the confidence interval of a proportion. The other two are the method of Wilson (4) and the hybrid Wilson/Brown method (5).

References

1. C. J. Clopper and E. S. Pearson, The use of confidence or fiducial limits illustrated in the case of the binomial, Biometrika 1934 26: 404-413.
2. RG Newcombe, Two-sided confidence intervals for the single proportion: Comparison of seven methods. Statistics in Medicine 17: 857-872, 1998.
3. Agresti, A., and Coull, B. A. (1998), Approximate is Better than "exact" for interval estimation of binomial proportions, The American Statistician, 52: 119-126.
4. Wilson, E. B. (1927). "Probable inference, the law of succession, and statistical inference". Journal of the American Statistical Association 22: 209–212. JSTOR 2276774.
5. Brown, L., Cai, T., & DasGupta, A. (2001). Interval Estimation for a Binomial Proportion. Statist. Sci, 16(2), 101–133.