Fixed Bug: Multiple comparison tests following two-way ANOVA with three or more columns. Fixed in 5.04 and 5.0d.
This bug is in Prism 4 and 5, and has been fixed in 5.04 (Windows) and 5.0d (Mac).
Summary: Following two-way ANOVA, Prism offers some multiple comparisons tests. The bug only occurs when you analyze three or more data set columns. In that case, Prism assigned multiple comparison significance too readily. Some of those comparisons that were labeled with an asterisk should not be. The confidence intervals are correct, and you can use the confidence intervals to correctly assign statistical signficance.
Two columns. Everything works fine.
Multiple comparison tests after two-way ANOVA are most often used when there are exactly two columns. The multiple comparison tests then compare one column vs. the other at each row.
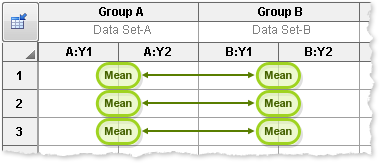
The number of comparisons in the family equals the number of rows. These comparisons are useful, and Prism reports the results correctly Both the confidence intervals and the significance levels properly adjust for multiple comparisons, and the two are consistent with each other. If the confidence interval does not include zero, that difference is statistically significant at the 5% level.
The bug described below only applies to three or more columns.
What is a family of comparisons following two-way ANOVA with three or more columns?
Prism 4 and 5 only offer two kinds of comparison. Within each row, it can compare each mean to every other mean on that row. Or it can compare every mean to the control mean (usually column A) on that row.
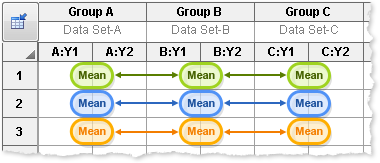
Multiple comparison calculations take into account the entire a family of comparisons, so the 95% confidence level and 5% significance level applies to the entire family. When the family of comparisons is large, it is requires a large difference to be considered statistically significant. Thus it is essential to carefully define the meaning of "family".
How is the family defined when there are three or more rows?Thus there are two possible definitions of a family of comparison:
- The comparisons on each row comprise a family of comparisons. There are as many families as there are rows.
- The family consists of all the comparisons in all the rows. There is only one family of comparisons for the entire ANOVA.
Prism uses the second definition, although we mistakenly wrote that it uses the first definition.
Are multiple comparison tests useful with three or more columns? Not always.
With three or more columns, the multiple comparison tests offered by Prism sometimes -- but not always -- correspond to useful scientific questions. Many investigators wisely skip multiple comparison testing when the two-way ANOVA has three or more data set columns. Before thinking about whether your results have been affected by this bug, first think carefully about whether the multiple comparisons tests are really useful at all.
Confidence intervals have always been correct. The problem is only with significance levels.
Prism reports the multiple comparison results as both confidence intervals and as significance levels. Many find that the confidence intervals are more useful. These have always been correct. There is no bug in the computation of multiple comparison corrected confidence intervals. The 95% confidence level applies to the entire family of intervals, not to each individually.
With three or more columns, Prism used a definition of statistical significance that is too liberal.
Prism (up to 5.03 and 5.0c) computed significance levels incorrectly for multiple comparisons after two-way ANOVA with three or more columns.
When deciding whether a particular difference is statistically significant or not (at a significance level you define), Prism needs to take into account the number of comparisons in the family. It incorrectly used the number of rows (Nrows) in this calculation, instead of the number of comparisons. Tthe bug occurred because with two columns, the number of comparisons is equal to the number of rows. When comparing every mean with every other mean (within each row), the actual number of comparisons is NRows*NCols*(NCols-1)/2. When comparing each mean vs. the control mean for that row, the actual number of comparisons is NRows*(Ncols-1).
Since Prism's adjustment for multiple comparisons is for fewer comparisons than were actually performed, it doesn't correct vigorously enough for multiple comparisons. Thus some of the "statistically significant" conclusions are incorrect, but all of the "not statistically significant" conclusions were correct. Overall, Prism has reported statistically significant results too often when reporting multiple comparisons tests following two-way ANOVA with three or more columns. Some comparisons labeled with a signficance asterisk should not have been so labeled.
Easy work around. How to know when a comparison is truly statistical significant.
Prism has always reported the confidence intervals correctly. So it is easy to tell if a comparison is statistically significant or not. Ignore the P values and asterisks reported by versions of Prism prior to 5.04 and 5.0d for two-way ANOVA multiple comparisons tests with three or more data set columns. Instead, follow these rules:
- If the 95% confidence interval for the difference between two means extends from a negative number to a positive number, and so includes 0.0, then that comparison is not statistically significant, and should not be labeled with an asterisk.
- In contrast, if the 95% confidence interval does not include 0.0, then that comparison is statistically significant, and should be labeled with an asterisk.
Keywords: Bonferroni, post tests















