Prism 3 -- How survival analyses work.
Prism 3 --
How survival analyses work
Introduction to survival curves
With many kinds of experiments, the outcome is a survival time and you wish to compare the survival of two or more groups. Prism creates survival curves, which plot percent survival as a function of time, using the method of Kaplan and Meier. Prism can also compare two or more survival curves using the logrank test.
The name survival curve is a bit misleading. The methods described in this chapter can analyze any kind of experiment where the result is expressed as a time to a well-defined end point. Instead of death, the endpoint could be occlusion of a vascular graft, first metastasis, or rejection of a transplanted kidney. The event does not have to be dire. The event could be restoration of renal function, discharge from a hospital, or graduation.
The end point must be a one-time event. Recurring events should not be analyzed with survival curves.
Some kinds of survival data are better analyzed with nonlinear regression. For example, don't use the methods in this chapter to analyze cell survival curves plotting percent survival (Y) as a function of various doses of radiation (X). The survival methods described in this chapter are only useful if X is time.
How survival analysis works
The fraction (or percent) survival at each time
Prism calculates survival fractions using the product limit or Kaplan-Meier method. For each X value (time) Prism shows the fraction still alive (or the fraction already dead, if you chose to begin the curve at 0.0 rather than 1.0). This table contains the numbers used to graph survival vs. time.
Prism also reports the uncertainty of the fractional survival as a standard error or 95% confidence intervals. Standard errors are calculated by the method of Greenwood. The 95% confidence intervals are computed as 1.96 times the standard error in each direction. In some cases the confidence interval calculated this way would start below 0.0 or end above 1.0 (or 100%). In these cases, the error bars are clipped to avoid impossible values.
On a second output view, Prism displays the number of patients still at risk at each time. As subjects die and are censored, the number still being followed decreases. This table also shows the median survival time for each group.
Logrank test to compare survival curves
If you entered two or more data sets in the table, Prism compares the survival curves and presents the comparison on a third output view.
Prism compares survival curves using the logrank test. If you entered two data sets, the logrank test is equivalent to the Mantel-Haenszel test. This test generates a P value testing the null hypothesis that the survival curves are identical in the overall populations. In other words, the null hypothesis is that the treatments did not change survival. The P value answers this question: If the null hypothesis is true, what is the probability of randomly selecting subjects whose survival curves are as different (or more so) than was actually observed?
Prism always calculates two-tailed P values. If you wish to report a one-tailed P value, you must have predicted which group would have the longer median survival before collecting any data. If your prediction was correct, the one-tail P value is half the two-tail P value. If your prediction was wrong, the one-tail P value is greater than 0.50, and you must conclude that the difference was due to chance, no matter how large it is.
Logrank test for trend
If you entered three or more data sets, Prism also calculates the logrank test for trend. This test is only meaningful if the data sets were entered in a logical order, perhaps corresponding to dose or age. If the data sets are not ordered (or not equally spaced), then you should ignore the results of the logrank test for trend. The logrank test for trend calculates a P value testing the null hypothesis that there is no linear trend between column number and median survival.
Median survival
The median survival is the time at which half the subjects have died. The example survival curve below shows 50% survival at 6 months, so median survival is 6 months.
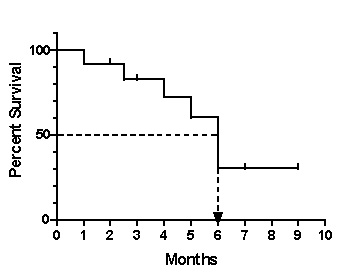
If survival exceeds 50% at the longest time points, then median survival cannot be computed. If the survival curve is horizontal at 50% survival, Prism reports the median survival as the average of the first and last times at which survival is 50%.
When comparing two survival curves, Prism also reports the ratio of the median survival times along with its 95% confidence interval. You can be 95% sure that the true ratio of median survival times lies within that range.
Hazard ratio
If you compare two survival curves, Prism reports the hazard ratio and its 95% confidence interval.
The hazard is the slope of the survival curve – a measure of how rapidly subjects are dying. The hazard ratio compares two treatments. If the hazard ratio is 2.0, then the rate of deaths in one treatment group is twice the rate in the other group.
The computation of the hazard ratio assumes that the ratio is consistent over time, and that any differences are due to random sampling. So Prism reports a single hazard ratio, not a different hazard ratio for each time interval. If two survival curves cross, the hazard ratios are not equal.
Reference for survival calculations
Most of the calculations are quite standard. Prism follows the calculations as spelled out in detail in DG Altman, Practical Statistics for Medical Research, 1991, Chapman and Hall.
For calculating the logrank test, Prism uses the second of the two methods described in that reference (more difficult to calculate, but more accurate). Some books call this method the Mantel-Haenszel logrank test.















