You'll use a different approach to compare nonlinear regression curve fits depending on whether you are comparing curves from one experiment or pool the results of several experiments.

Compare best-fit values pooled from several experiments

The best way to compare best-fit values is to repeat the experiment several times, and then analyze the pooled data. The first step is to focus on what you really want to know. For dose-response curves, you may want to test whether the two EC50 values differ significantly, whether the maximum responses differ, or both.  With kinetic curves, you'll want to ask about differences in rate constants or maximum response. With other kinds of experiments, you may summarize the experiment in other ways, perhaps as the maximum response, the minimum response, the time to maximum, the slope of a linear regression line, etc. Or perhaps you want to integrate the entire curve and use area-under-the-curve as an overall measure of cumulative response.

Once you've summarized each curve as a single value, compare those values using a paired t test.

For example, below are the results of a binding study to determine receptor number (Bmax). The experiment was performed three times with control and treated cells side-by-side. Each value is a Bmax determined by nonlinear regression.

Experiment	Control	Treated
1	1234	987
2	1654	1324
3	1543	1160

 

Treat the Bmax values determined from nonlinear regression just as you'd treat any measurement, and compare the two groups with a t test. Because control and treated cells were treated side-by-side to control for experiment-to-experiment variability, analyze the data using a paired t test.

 

The two-tailed P value is 0.0150, so the effect of the treatment on reducing receptor number can be deemed "statistically significant". The 95% confidence interval of the decrease in receptor number ranges from 149.70 to 490.30 sites/cell.

These calculations were based only on the best-fit Bmax values, ignoring all the other results calculated by the curve-fitting program. You may be concerned that you are not making best use of the data, since the number of points and replicates do not appear to affect the calculations. But they do contribute indirectly. You'll get more accurate results if you use more concentrations of ligand in each experiment, so the results of the experiments will be more consistent. If there really are differences between control and treated curves, you'll get a higher t ratio and a lower P value if you use more concentrations.

If you have three or more treatment groups, use repeated measures one-way ANOVA rather than a paired t test.

Compare two best-fit values from one experiment

t test approach

Even if you've done the experiment only once, you can compare the best-fit values of two groups using a t test. A t test compares a difference with the standard error of that difference. That standard error can come by pooling several experiments (as in the previous approach) or you can use the standard error reported by nonlinear regression. For example, here are the results of first experiment in Approach 1.

	Best-fit Bmax	SE	df
Control	1234	98	14
Treated	987	79	14

Calculate the unpaired t test using this equation:

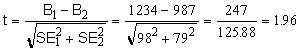
The numerator is the difference between best-fit values. The denominator is an estimate of the standard error of that difference, computed as the square root of the sum of the squares of the two standard error values. This is a reasonable estimate if the number of data points in the two curves is equal, or nearly so. If the sample sizes are very different, don't rely on this calculation.

To determines the two-tailed P value from t, you need to know the number of degrees of freedom. Each fit in this example has 14 degrees of freedom (equal to the number of data points minus the number of variables fit). The t test in this example has 28 degrees of freedom, the sum of the degrees of freedom in each fit. Determine the P value using a program or the excel formula "=tdist(1.96,28,2)" . The two-tailed P value corresponding to t=1.96 and df=28 is 0.06. If there really were no difference between Bmax values, you'd see a difference this large or larger in 6% of experiments of this size. Using the conventional threshold of P=0.05, the difference between Bmax values in this example is not statistically significant.

The use of a t test to compare best-fit values (pooling several experiments or within one experiment) depends on the assumption that the distribution of best-fit values follows a Gaussian distribution. If you were to repeat the experiment many times, the distribution of the best-fit values must follow a Gaussian distribution. With linear regression, this assumption is sure to be valid if your data obey all the assumptions of the analysis. With nonlinear regression, the best-fit values may not be Gaussian, even if the data follow all the assumptions.

Compare by global fitting

Prism makes it easy to compare fits by global fitting. Your data must be all on one data table, with two (or more) data sets. Click Analyze, choose nonlinear regression, and choose the model you want to fit. Then go to the compare tab, and specify the comparison you want. These pages in the Prism help explain this approach.

Overview

F test or AICc?

The Compare tab of nonlinear regression dialog

Interpreting comparisons

Comparing slopes and intercepts of linear regression

Zar details a special method to compare the slopes and intercepts of two regression lines in Chapter 18 of J Zar, Biostatistical Analysis, 2nd edition, Prentice-Hall, 1984.  You'll need to read Zar's book to do the calculations yourself, but the basic idea is straightforward. Compare the slopes first, testing the null hypothesis that the slopes are all identical (the lines are parallel). The P value answers this question: If the slopes really were identical, what is the chance that randomly selected data points would have slopes as different (or more different) than you observed. If the P value is less than 0.05, conclude that the lines are significantly different. In that case, there is no point in comparing the intercepts. The intersection point of two lines is:

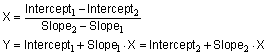
If the P value for comparing slopes is greater than 0.05, conclude that the slopes are not significantly different. Now  calculate a single slope for both lines. Now the question is whether the lines are parallel or identical. Prism calculates a second P value testing the null hypothesis that the lines are identical. If this P value is low, conclude that the lines are not identical (they are distinct but parallel). If this second P value is high, there is no compelling evidence that the lines are different.

This method is equivalent to an Analysis of Covariance (ANCOVA), although ANCOVA can be extended to more complicated situations.  

GraphPad Prism uses this method to compare two linear regression lines.

Two-way ANOVA to compare curves, without a model

It is also possible to compare two curves, without fitting a model using two-way ANOVA. The two factors are treatment and whatever variable is coded by X (usually time or concentration). One of the P values from ANOVA tests the null hypothesis that treatment had no effect on the outcome Y. If this P value is small, you conclude that the treatment made a difference overall. You can compare Y values at each value of X, using post tests following two-way ANOVA.