How can I determine an EC90 (or any EC value other than EC50)?
The potency of a drug is commonly quantified as the EC50, the concentration that leads to 50% maximal response (or the logarithm of the EC50). But in some systems you might be more interested in the EC80 or the EC90 or some other value. You can either compute these values from the EC50 or fit a curve in such a way as to directly fit ECanything.
Use a free web calculator
One of our free web calculators does the calculation for you. Enter the EC50 and Hill Slope and it will calculate whatever EC value you want.
ComputingECanythingfrom the EC50
If you've already obtained an EC50 value by nonlinear regression in Prism and you don't need an error estimate, use this equation to determine ECF (where F might be 80 or 90 ...) from the EC50 and Hill Slope (H):
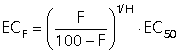
(This equation was derived by starting with the equation that defines percent response F, from EC50, H, and concentration, and then rearranging to solve for the concentration (ECF).)
If you know the EC50 and Hill slope (H), you can easily compute the EC80 or EC10 or any other value you want. For example, if the Hill slope equals 1, the EC90 equals the EC50 times nine. If H equals 0.5, the curve is shallower and the EC90 equals the EC50 times 81.
Fitting the ECanything directly using Prism
You can fit data directly to an equation written in terms of the ECF, where F=fraction of maximal response (example: for EC90, F=90). The advantage of this approach is that Prism will report the 95% confidence value for ECF.
The needed equation is built in to Prism starting with version 5. Details.
ICanything
If your response goes down with increasing dose (so the Hill slope is negative), watch out for the terminology. The EC10 (for example) is defined as the concentration that gives you a response 10% of the way between the Bottom and Top plateaus. In situations where the response goes down as you increase dose, you may think of this as the "IC90" since it gives 90% of the maximum inhibition.
Another example. Let's say you set F=80. Then the ECf for inhibitory data would be the concentration (X value) required to bring the curve down to 80%. If you actually want the concentration that brings the curve down by 80%, to 20%, then you'd need to set F equal to 20.
What if the dose-response curve is incomplete?
When a dose-response curve is incomplete, then the determination of a value on the curve is not accurate. If you can not define the top and bottom plateaus of a curve, then it is not possible to determine other regions of the curve that are defined by their relationship to the top and bottom plateaus. This point is discussed further in a section of FAQ 1356.
What about EC100?
As the concentration (X) goes up, the dose-response equation computes the response (Y) as getting closer and closer to the Top plateau. But it never reaches it. When a drug binds to a receptor with mass action rules, the fraction occupancy equals D/(D+K), where D is the concentration of drug (that you vary) and K is the equilibrium binding dissioction constant, which is a fixed property of the drug and receptor. As D gets higher and higher, the fractional occupancy gets closer and closer to 1.0, but never reaches it. Therefore, there can be no EC100. And no EC0.
For early releases of Prism (or other programs):
If you are using Prism 4 or earlier, you will need to write your own equation. From the table (if you entered your data as log of concentration) or results sheet (if Prism did the log transformation for you), initiate a nonlinear regression analysis. In the "Parameters" dialog, choose "More equations" and then select "[Enter your own equation]" from the list. In the "Equation" dialog, give your equation a name you'll recognize, then enter this equation set:
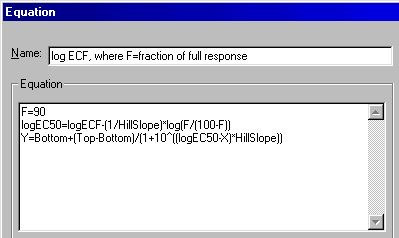
Click "Rules for Initial Values" and tell Prism how to derive the initial values for the curve fit. Note that we're setting up the analysis described under Determining any EC value directly at curvefit.com:
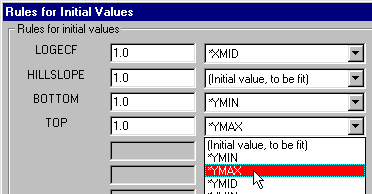
Click "OK" three times to back out of these dialogs and perform the curve fit. Prism displays a results sheet showing the best fit value, the standard error, and the 95% confidence interval for the ECF, or in this case, the EC90.
Here are some additional tips:
- Notice that the equation name will show up among your choices under "More equations" the next time you want to do the analysis.
- If you occasionally want a different ECF, you can edit the equation, changing the value of F.
- If you're always interested in the same value of F, you can simplify the equations. Here is the simplified equation set for EC90 (note that the results sheet will now explicitly display "logEC90"):
Y=Bottom + (Top-Bottom)/(1+10^((LogEC50-X)*HillSlope))
Of course, you can always set up multiple ECF analyses, based upon different F values, using the simplified equations.
Keywords: user defined user-defined EC10 EC20 EC25 EC30 EC40 EC50 EC60 EC70 EC75 EC80 EC90 IC10 IC20 IC25 IC30 IC40 IC50 IC60 IC70 IC75 IC80 IC90 ED10 ED20 ED25 ED30 ED40 ED50 ED60 ED70 ED75 ED80 ED90 LD10 LD20 LD25 LD30 LD40 LD50 LD60 LD70 LD75 LD80 LD90















